本文是《热力学与统计物理》第三章内容

三、单元系的相变

3.0 热动平衡的条件
3.1 热动平衡判据
3.2 开系的热力学基本方程
3.3 单元系的复相平衡条件
3.4 单元复相系的平衡性质
3.5 临界点和气液两相的转变
3.7 相变的分类
3.9 朗道连续相变理论

3.0 热动平衡的条件

弛豫机理:

  • 分子之间的碰撞
  • 分子与器壁之间的作用

3.1 热动平衡判据

热平衡的判据（热动平衡条件）
（1）基本平衡判据
熵判据：孤立系统平衡态是熵最大的态。
相对于平衡态的虚变动后的态的熵变小。
孤立系统处在稳定平衡状态的必要充分条件: ΔS<0\Delta S < 0

变分展开式：ΔS=δS+12!δ2S+13!δ3S+⋯\Delta S=\delta S+\frac{1}{2!} \delta^2 S+\frac{1}{3!} \delta^3 S+\cdots
平衡条件：δS=0\delta S = 0 (是变分，不是微分)。
稳定平衡： δ2S<0\delta^2 S<0
非稳平衡： δ2S>0\delta^2 S>0
亚稳平衡： δ2S<0\delta^2 S<0,SS非最大
中性平衡： δ2S=0;δ3S=0;…\delta^2 S=0 ; \quad \delta^3 S=0 ; \quad \ldots

统计规律要成立，宏观规律要成立

τ弛豫=V1/3v弛豫→V→00\tau_{\text {弛豫}}=\frac{V^{1 / 3}}{v_{\text {弛豫}}} \quad \xrightarrow{V \rightarrow 0} 0

二级平衡判据
（1）等温等容系统——自由能判据
平衡态是熵最大的态 ⟹\Longrightarrow 平衡态自由能最小
F=U−TS⟹ΔF>0F=U-T S \Longrightarrow \Delta F>0

平衡条件：δF=0\delta F=0
稳定平衡：δ2F=0\delta^2 F=0

（2）等温等压系统——吉布斯判据
平衡态是熵最大的态 ⟹\Longrightarrow 平衡态吉布斯函数最小
G=U−TS+PV⟹ΔG>0G=U-T S+P V \Longrightarrow \Delta G>0

平衡条件：δG=0\delta G=0
稳定平衡：δ2G=0\delta^2 G=0

同理可得不同条件下物理系统的平衡判据。

均匀系统热动平衡条件

对于孤立的均匀系统,系统的体积V不变，内能U不变。
子系统虚变动和系统其余部分虚变动满足：

δU0+δU=0δV0+δV=0\begin{aligned} & \delta U_0+\delta U=0 \\ & \delta V_0+\delta V=0 \end{aligned}

系统总熵变：

ΔS~=ΔS0+ΔS≈δS~+12δ2S~\Delta \tilde{S}=\Delta S_0+\Delta S \approx \delta \tilde{S}+\frac{1}{2} \delta^2 \tilde{S}

ΔS0≈δS0+12δ2S0,ΔS≈δS+12δ2S\Delta S_0 \approx \delta S_0+\frac{1}{2} \delta^2 S_0 \quad, \Delta S \approx \delta S+\frac{1}{2} \delta^2 S

系统的平衡条件：δS~=δS+δS0=0\delta \tilde{S}=\delta S+\delta S_0=0

根据

δS=δU+pδVT,δS0=δU0+p0δV0T0=−δU+p0δVT0\delta S=\frac{\delta U+p \delta V}{T} \quad, \delta S_0=\frac{\delta U_0+p_0 \delta V_0}{T_0}=-\frac{\delta U+p_0 \delta V}{T_0}

代入平衡条件得到：

δS~=δU(1T−1T0)+δV(pT−p0T0)=0\delta \tilde{S}=\delta U\left(\frac{1}{T}-\frac{1}{T_0}\right)+\delta V\left(\frac{p}{T}-\frac{p_0}{T_0}\right)=0

由于虚变动δU,δV\delta U,\delta V可任意变化，故上式要求：

T=T0,p=p0T = T_0 , p = p_0

结果表明：达到平衡时整个系统的温度和压强是均匀的

稳定平衡: δ2S~=δ2S0+δ2S<0\delta^2 \tilde{S}=\delta^2 S_0+\delta^2 S<0
近似有 δ2S~≈δ2S<0\delta^2 \tilde{S} \approx \delta^2 S<0

从而要求：

δ2S=∂2S∂U2(δU)2+2∂2S∂U∂VδUδV+∂2S∂V2(δV)2<0\delta^2 S=\frac{\partial^2 S}{\partial U^2}(\delta U)^2+2 \frac{\partial^2 S}{\partial U \partial V} \delta U \delta V+\frac{\partial^2 S}{\partial V^2}(\delta V)^2<0

上式转化为：δ2S=−CVT2(δT)2+1T(∂p∂V)T(δV)2<0\delta^2 S=-\frac{C_V}{T^2}(\delta T)^2+\frac{1}{T}\left(\frac{\partial p}{\partial V}\right)_T(\delta V)^2<0

证明：S=S(U,V),dS=(∂S∂U)VdU+(∂S∂V)UdVS=S(U, V) \quad ,d S=\left(\frac{\partial S}{\partial U}\right)_V d U+\left(\frac{\partial S}{\partial V}\right)_U d V

d2S=d[(∂S∂U)VdU]+d[(∂S∂V)UdV]=(∂2S∂U2)V(dU)2+(∂2S∂U∂V)dVdU+(∂2S∂V2)U(dV)2+(∂2S∂U∂V)dVdU=(∂2S∂U2)V(dU)2+2(∂2S∂U∂V)dVdU+(∂2S∂V2)U(dV)2\begin{aligned} & d^2 S=d\left[\left(\frac{\partial S}{\partial U}\right)_V d U\right]+d\left[\left(\frac{\partial S}{\partial V}\right)_U d V\right] \\ & =\left(\frac{\partial^2 S}{\partial U^2}\right)_V(d U)^2+\left(\frac{\partial^2 S}{\partial U \partial V}\right) d V d U+\left(\frac{\partial^2 S}{\partial V^2}\right)_U(d V)^2+\left(\frac{\partial^2 S}{\partial U \partial V}\right) d V d U \\ & =\left(\frac{\partial^2 S}{\partial U^2}\right)_V(d U)^2+2\left(\frac{\partial^2 S}{\partial U \partial V}\right) d V d U+\left(\frac{\partial^2 S}{\partial V^2}\right)_U(d V)^2 \end{aligned}

d→δ⟶δ2S=∂2S∂U2(δU)2+2∂2S∂U∂VδUδV+∂2S∂V2(δV)2=[∂∂U(∂S∂U)δU+∂∂V(∂S∂U)δV]δU+[∂∂U(∂S∂V)δU+∂∂V(∂S∂V)δV]δV\begin{aligned} & d \rightarrow \delta \longrightarrow \delta^2 S=\frac{\partial^2 S}{\partial U^2}(\delta U)^2+2 \frac{\partial^2 S}{\partial U \partial V} \delta U \delta V+\frac{\partial^2 S}{\partial V^2}(\delta V)^2 \\ & =\left[\frac{\partial}{\partial U}\left(\frac{\partial S}{\partial U}\right) \delta U+\frac{\partial}{\partial V}\left(\frac{\partial S}{\partial U}\right) \delta V\right] \delta U+\left[\frac{\partial}{\partial U}\left(\frac{\partial S}{\partial V}\right) \delta U+\frac{\partial}{\partial V}\left(\frac{\partial S}{\partial V}\right) \delta V\right] \delta V \end{aligned}

TdS=dU+pdV⟹(∂S∂U)V=1T,(∂S∂V)U=pTT d S=d U+p d V \quad \Longrightarrow\left(\frac{\partial S}{\partial U}\right)_V=\frac{1}{T}, \quad\left(\frac{\partial S}{\partial V}\right)_U=\frac{p}{T}

⟹δ2S=[∂∂U(1T)δU+∂∂V(1T)δV]δU+[∂∂U(pT)δU+∂∂V(pT)δV]δV=δ(1T)δU+δ(pT)δV\begin{aligned} \Longrightarrow & \delta^2 S=\left[\frac{\partial}{\partial U}\left(\frac{1}{T}\right) \delta U+\frac{\partial}{\partial V}\left(\frac{1}{T}\right) \delta V\right] \delta U+\left[\frac{\partial}{\partial U}\left(\frac{p}{T}\right) \delta U+\frac{\partial}{\partial V}\left(\frac{p}{T}\right) \delta V\right] \delta V \\ & =\delta\left(\frac{1}{T}\right) \delta U+\delta\left(\frac{p}{T}\right) \delta V \end{aligned}

以T,V为自变量：U=U(T,V)U=U(T, V)

δU=(∂U∂T)VδT+(∂U∂V)TδV=CVδT+[T(∂p∂T)V−p]δVδ(1T)=(∂∂T1T)VδT+(∂∂V1T)TδV=−1T2δTδ(pT)=(∂∂TpT)VδT+(∂∂VpT)TδV=1T2[T(∂p∂T)V−p]δT+1T(∂p∂V)TδV\begin{aligned} & \delta U=\left(\frac{\partial U}{\partial T}\right)_V \delta T+\left(\frac{\partial U}{\partial V}\right)_T \delta V=C_V \delta T+\left[T\left(\frac{\partial p}{\partial T}\right)_V-p\right] \delta V \\ & \delta\left(\frac{1}{T}\right)=\left(\frac{\partial}{\partial T} \frac{1}{T}\right)_V \delta T+\left(\frac{\partial}{\partial V} \frac{1}{T}\right)_T \delta V=-\frac{1}{T^2} \delta T \\ & \delta\left(\frac{p}{T}\right)=\left(\frac{\partial}{\partial T} \frac{p}{T}\right)_V \delta T+\left(\frac{\partial}{\partial V} \frac{p}{T}\right)_T \delta V=\frac{1}{T^2}\left[T\left(\frac{\partial p}{\partial T}\right)_V-p\right] \delta T+\frac{1}{T}\left(\frac{\partial p}{\partial V}\right)_T \delta V \end{aligned}

δ2S=−CVT2(δT)2+1T(∂p∂V)T(δV)2<0\delta^2 S=-\frac{C_V}{T^2}(\delta T)^2+\frac{1}{T}\left(\frac{\partial p}{\partial V}\right)_T(\delta V)^2<0

此即平衡的稳定条件

上页得到：δ2S=−CVT2(δT)2+1T∂p∂V∣T(δV)2<0\delta^2 S=-\frac{C_V}{T^2}(\delta T)^2+\left.\frac{1}{T} \frac{\partial p}{\partial V}\right|_T(\delta V)^2<0

V,T 相互独立，T>0，故要求：
CV>0,(∂p∂V)T<0C_V>0 \quad , \left(\frac{\partial p}{\partial V}\right)_T<0 \quad 平衡的稳定条件

讨论:

  • 子系统温度略高于媒质：由平衡条件，子系统传递热量而使温度降低，于是子系统恢复平衡；
  • 子系统体积收缩：由平衡条件，子系统的压强将增加，于是子系统膨胀而恢复平衡。

3.2 开系的热力学基本方程

（1）基本概念
相：热力学系统中物理性质均匀的部分。
水、汽 -- 不同的相；铁磁、顺磁 -- 不同的相。

单元系:化学上纯的物质系统,只含一种化学组分(一个组元).

复相系:系统不是均匀的,但可以分为若干个均匀的部分
水和水蒸气共存---单元两相系;冰,水和水蒸气共存---单元三相系

相变：一个相到另一个相的转变。通常发生在等温等压的情况（p-T图）

与封闭系统比较，开放系统的物质的量 n 可能发生变化。研究气－液相变，每一相可以看作一个开放系统。

这样的系统除了均匀系统需要两个状态参量外，增加了一个独立变化的参量－摩尔数。

(T,p)→(T,p,n)(T, p) \rightarrow(T, p, n)

摩尔数与系统的广延性相关。系统的吉布斯函数依赖于两个强度量: 温度和压强

G(T,p)=U−TS+pVG(T, p)=U-T S+p V

但它是广延量，它将随摩尔数改变而改变。它的改变量应正比于摩尔数改变量

G(T,p,n)=U−TS+pVG(T, p, n)=U-T S+p V

（2）热力学基本方程

dG=−SdT+Vdp+μdnd G=-S d T+V d p+\mu d n

μ=(∂G∂n)T,p\mu=\left(\frac{\partial G}{\partial n}\right)_{T, p}叫系统的化学势。

系统的吉布斯函数与其摩尔数成正比

G(T,p,n)=nGm(T,p)μ=∂G∂n∣T,p=Gm(T,p)G(T, p, n)=n G_m(T, p) \quad \mu=\left.\frac{\partial G}{\partial n}\right|_{T, p}=G_m(T, p)

已知特性函数G(T,p,n)G(T,p,n),可求得

S=−(∂G∂T)p,n,V=(∂G∂p)T,n,μ=(∂G∂n)T,pS=-\left(\frac{\partial G}{\partial T}\right)_{p, n}, \quad V=\left(\frac{\partial G}{\partial p}\right)_{T, n}, \mu=\left(\frac{\partial G}{\partial n}\right)_{T, p}

同样，其他热力学基本方程有：

dU=TdS−pdV+μdnμ=(∂U∂n)S,VdH=TdS+Vdp+μdnμ=(∂H∂n)S,pdF=−SdT−pdV+μdnμ=(∂F∂n)T,V\begin{array}{ll} d U=T d S-p d V+\mu d n & \mu=\left(\frac{\partial U}{\partial n}\right)_{S, V} \\ d H=T d S+V d p+\mu d n & \mu=\left(\frac{\partial H}{\partial n}\right)_{S, p} \\ d F=-S d T-p d V+\mu d n & \mu=\left(\frac{\partial F}{\partial n}\right)_{T, V} \end{array}

定义巨热力势：J=F−μNJ=F-\mu N
全微分：dJ=−SdT−pdV−ndμd J=-S d T-p d V-n d \mu

JJ 是以T,V,μT,V,μ为独立变量的特性函数，可以认为是 FF 的推广：

S=−(∂J∂T)V,μ,p=−(∂J∂V)T,μ,n=−(∂J∂μ)T,VS=-\left(\frac{\partial J}{\partial T}\right)_{V, \mu}, \quad p=-\left(\frac{\partial J}{\partial V}\right)_{T, \mu}, \quad n=-\left(\frac{\partial J}{\partial \mu}\right)_{T, V}

巨热力势JJ也可表为:

J=F−G=−pVG=nGm=nμJ=F-G=-p V \quad G=n G_m=n \mu

3.3 单元系的复相平衡条件

（1）单元复相系：一种成分，两个相
（2）相平衡条件 δS=0\delta S = 0

δS=δSα+δSβ=δUα(1Tα−1Tβ)+δVα(pαTα−pβTβ)−δnα(μαTα−μβTβ)⇒1Tα−1Tβ=0pαTα−pβTβ=0μαTα−μβTβ=0\begin{gathered} \delta S=\delta S_\alpha+\delta S_\beta=\delta U_\alpha\left(\frac{1}{T_\alpha}-\frac{1}{T_\beta}\right)+\delta V_\alpha\left(\frac{p_\alpha}{T_\alpha}-\frac{p_\beta}{T_\beta}\right)-\delta n_\alpha\left(\frac{\mu_\alpha}{T_\alpha}-\frac{\mu_\beta}{T_\beta}\right) \\ \Rightarrow \quad \frac{1}{T_\alpha}-\frac{1}{T_\beta}=0 \quad \frac{p_\alpha}{T_\alpha}-\frac{p_\beta}{T_\beta}=0 \quad \frac{\mu_\alpha}{T_\alpha}-\frac{\mu_\beta}{T_\beta}=0 \end{gathered}

热平衡条件: Tα=TβT_\alpha=T_\beta
力学平衡条件: pα=pβp_\alpha=p_\beta
相变平衡条件: μα=μβ\mu_\alpha=\mu_\beta

（3）趋向平衡的方向

 非平衡 →δS>0 熵增加  平衡 \text { 非平衡 } \xrightarrow[\delta S>0]{\text { 熵增加 }} \text { 平衡 }

δS=δSα+δSβ=δUα(1Tα−1Tβ)+δVα(pαTα−pβTβ)−δnα(μαTα−μβTβ)>0\delta S=\delta S_\alpha+\delta S_\beta=\delta U_\alpha\left(\frac{1}{T_\alpha}-\frac{1}{T_\beta}\right)+\delta V_\alpha\left(\frac{p_\alpha}{T_\alpha}-\frac{p_\beta}{T_\beta}\right)-\delta n_\alpha\left(\frac{\mu_\alpha}{T_\alpha}-\frac{\mu_\beta}{T_\beta}\right)>0

热平衡方向：

δUα(1Tα−1Tβ)>0⇒δUα(Tβ−Tα)>0⇒δUα>0Tβ−Tα>0\delta U_\alpha\left(\frac{1}{T_\alpha}-\frac{1}{T_\beta}\right)>0 \Rightarrow \delta U_\alpha\left(T_\beta-T_\alpha\right)>0 \Rightarrow \begin{aligned} & \delta U_\alpha>0 \\ & T_\beta-T_\alpha>0 \end{aligned}

热量传递方向：热量从高温相向低温相传递

力学平衡方向：

δVα(pαTα−pβTβ)>0⇒Tα=TβδVα(pα−pβ)>0⇒δVα>0pα>pβ\delta V_\alpha\left(\frac{p_\alpha}{T_\alpha}-\frac{p_\beta}{T_\beta}\right)>0 \Rightarrow \begin{gathered} T_\alpha=T_\beta \\ \delta V_\alpha\left(p_\alpha-p_\beta\right)>0 \end{gathered} \quad \Rightarrow \begin{gathered} \delta V_\alpha>0 \\ p_\alpha>p_\beta \end{gathered}

体积膨胀方向：压强大的相体积膨胀，压强小的相将被压缩。

相变平衡方向：

−δnα(μαTα−μβTβ)>0⇒Tα=Tβδnα(μα−μβ)<0⇒μα>μβδnα<0-\delta n_\alpha\left(\frac{\mu_\alpha}{T_\alpha}-\frac{\mu_\beta}{T_\beta}\right)>0 \Rightarrow \begin{gathered} T_\alpha=T_\beta \\ \delta n_\alpha\left(\mu_\alpha-\mu_\beta\right)<0 \end{gathered} \quad \Rightarrow \begin{gathered} \mu_\alpha>\mu_\beta \\ \delta n_\alpha<0 \end{gathered}

⟹\Longrightarrow粒子方向:粒子从化学势高的相向低的相跑

3.4 单元复相系的平衡性质

（1）气－液相变

相图

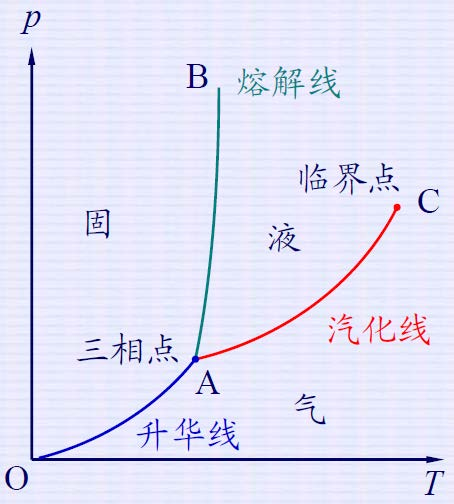
AC: 汽化曲线；
AB: 熔解曲线；
AO: 升华曲线。
A ：三相点
C ：临界点。

水：
临界温度：647.05K
临界压强：22.09×106 Pa
三相点：T=273.16K，P=610.9 Pa

在曲线上，T,p,μ(T,p)T,p,\mu(T,p)相等，不在曲线上，μ\mu更小的态存在
即等温等压下，系统的平衡状态，一定是化学势最小的状态。

（2）克拉珀龙方程

利用相平衡性质，导出克拉珀龙方程

考虑相平衡性质，相平衡曲线上有

μα(T,p)=μβ(T,p)\mu_\alpha(T, p)=\mu_\beta(T, p)

μα(T+dT,p+dp)=μβ(T+dT,p+dp) \mu_\alpha(T+d T, p+d p) = \mu_\beta(T+d T, p+d p)

相减:

dμα=dμβd \mu_\alpha=d \mu_\beta

dμ=dGm=−SmdT+Vmdpd \mu=d G_m=-S_m d T+V_m d p

得：

−Sm,αdT+Vm,αdp=−Sm,βdT+Vm,βdp -S_{m, \alpha} d T+V_{m, \alpha} d p = -S_{m, \beta} d T+V_{m, \beta} d p

有：

dpdT=Sm,β−Sm,αVm,β−Vm,α\frac{d p}{d T}=\frac{S_{m, \beta}-S_{m, \alpha}}{V_{m, \beta}-V_{m, \alpha}}

定义潜热：

L=T(Sm,β−Sm,α)L=T\left(S_{m, \beta}-S_{m, \alpha}\right)

克拉珀龙方程：

dpdT=LT(Vm,β−Vm,α)\frac{d p}{d T}=\frac{L}{T\left(V_{m, \beta}-V_{m, \alpha}\right)}

（3）蒸气压方程
饱和蒸气: 与凝聚相(液相或固相)达到平衡的蒸气
蒸气压方程: 描述饱和蒸气压与温度的关系的方程
设 α\alpha :凝聚相 , β\beta :气相，则

Vm,α<<Vm,βpVm,β=RTV_{m, \alpha}<<V_{m, \beta} \quad p V_{m, \beta}=R T

代入克拉珀龙方程可得：

1pdpdT=LRT2\frac{1}{p} \frac{d p}{d T}=\frac{L}{R T^2}

近似L与T无关，有:

ln⁡p=−LRT+A\ln p=-\frac{L}{R T}+A

3.5 临界点和气液两相的转变

范德瓦耳斯方程

(p+aVm2)(Vm−b)=RT\left(p+\frac{a}{V_m^2}\right)\left(V_m-b\right)=R T

在μ−p\mu -p图上，可看到，1个pp对应3个μ\mu值，由吉布斯函数最小的判据，知OKBAMR是稳定平衡状态。

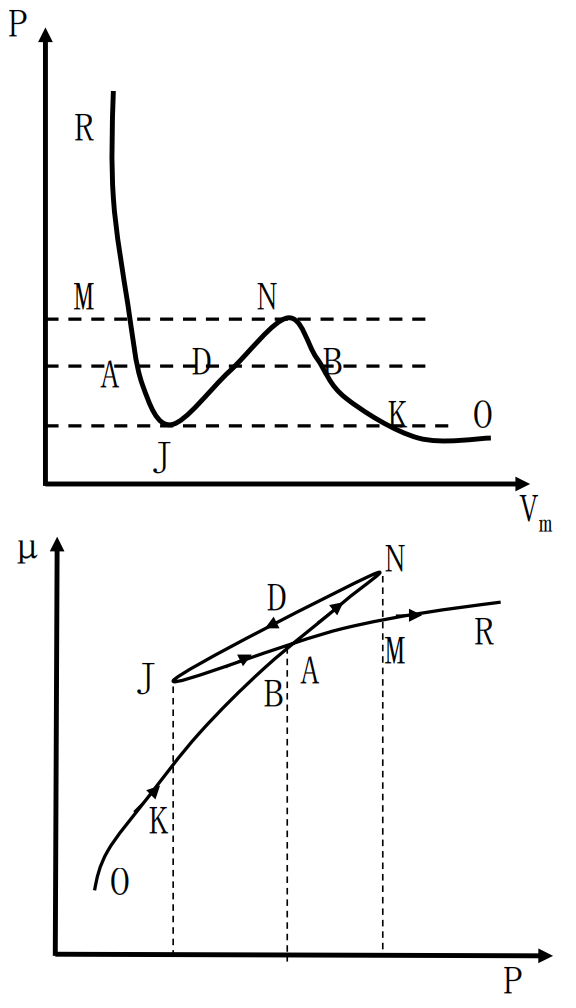
μ=Gm(T,p)=U−TS+pVdμ=−SmdT+Vmdp\mu=G_m(T, p)=U-T S+p V \quad d \mu=-S_m d T+V_m d p

等温条件:

dμ=Vmdpd \mu = V_m d p

⟹μ−μ0=∫p0pVmdpμA=μB,μA−μB=∫BNDJAVmdp=0\begin{aligned} & \Longrightarrow \mu-\mu_0=\int_{p_0}^p V_m d p \\ & \mu_A=\mu_B, \quad \mu_A-\mu_B=\int_{B N D J A} V_m d p=0 \end{aligned}

⟹SBND=SDJA\Longrightarrow S_{BND} = S_{DJA}

  • AM（液）：稳定
  • BN（气）：亚稳（过饱和）
  • BK（气）：稳定
  • AJ（液）：亚稳（过热）

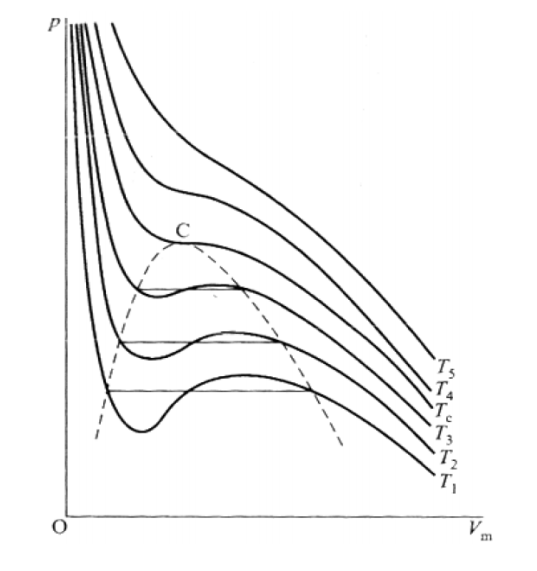
临界点：

  • 极小点：∂p∂Vm∣T=0∂2p∂Vm2∣T>0\left.\frac{\partial p}{\partial V_m}\right|_T=\left.0 \quad \frac{\partial^2 p}{\partial V_m{ }^2}\right|_T>0
  • 极大点:∂p∂Vm∣T=0∂2p∂Vm2∣T<0\left.\frac{\partial p}{\partial V_m}\right|_T=\left.0 \quad \frac{\partial^2 p}{\partial V_m{ }^2}\right|_T<0
  • 拐点：T→TCT \rightarrow T_C,即∂p∂Vm∣T=0∂2p∂Vm2∣T=0\left.\frac{\partial p}{\partial V_m}\right|_T=\left.0 \quad \frac{\partial^2 p}{\partial V_m{ }^2}\right|_T=0

由范德瓦尔斯方程:

p=RTVm−b−aVm2p=\frac{R T}{V_m-b}-\frac{a}{V_m{ }^2}

∂p∂Vm∣T=−RT(Vm−b)2+2aVm3∂2p∂Vm2∣T=2RT(V−b)3−6aVm4\left.\frac{\partial p}{\partial V_m}\right|_T=-\frac{R T}{\left(V_m-b\right)^2}+\left.\frac{2 a}{V_m^3} \quad \frac{\partial^2 p}{\partial V_m{ }^2}\right|_T=\frac{2 R T}{(V-b)^3}-\frac{6 a}{V_m^4}

结合范式方程，得：

Tc=8a27Rb,pc=a27b2,Vmc=3bT_c=\frac{8 a}{27 R b}, \quad p_c=\frac{a}{27 b^2}, \quad V_{m c}=3 b

RTcpcVmc=83=2.667\frac{R T_c}{p_c V_{m c}}=\frac{8}{3}=2.667

引进新变量t∗=TTc,p∗=ppc,v∗=VmVmct^*=\frac{T}{T_c}, \quad p^*=\frac{p}{p_c}, \quad v^*=\frac{V_m}{V_{m c}}，得

(p∗+3v∗2)(v∗−13)=83t∗\left(p^*+\frac{3}{v^{* 2}}\right)\left(v^*-\frac{1}{3}\right)=\frac{8}{3} t^*

称为范氏对比方程

对应态定律：一切物质在相同的对比压强和对比温度下，就有相同的对比体积，即采用对比变量，各种气（液）体的物态方程是完全相同的。

3.7 相变的分类

前面所讲的固、气、液相变有相变潜热和体积变化，但还有一类相变，如气--液通过临界点的转变，铁磁顺磁相变，合金有序无序转变等等，无相变潜热和体积变化。1933年，Ehrenfest对相变进行分类。

A:一级相变:
相平衡时,化学势连续

μ(1)(T,p)=μ(2)(T,p)\mu^{(1)}(T, p)=\mu^{(2)}(T, p)

考虑到

dμ=−SmdT+Vmdps=−(∂μ∂T)p,v=(∂μ∂p)T\begin{gathered} d \mu=-S_m d T+V_m d p \\ s=-\left(\frac{\partial \mu}{\partial T}\right)_p, v=\left(\frac{\partial \mu}{\partial p}\right)_T \end{gathered}

有

∂μ(1)∂T≠∂μ(2)∂T(s(1)≠s(2))\frac{\partial \mu^{(1)}}{\partial T} \neq \frac{\partial \mu^{(2)}}{\partial T}\left(s^{(1)} \neq s^{(2)}\right)

∂μ(1)∂p≠∂μ(2)∂p(v(1)≠v(2))\frac{\partial \mu^{(1)}}{\partial p} \neq \frac{\partial \mu^{(2)}}{\partial p}\left(v^{(1)} \neq v^{(2)}\right)

一般性质:
一级相变,两相不同的斜率－不同的熵、比容。

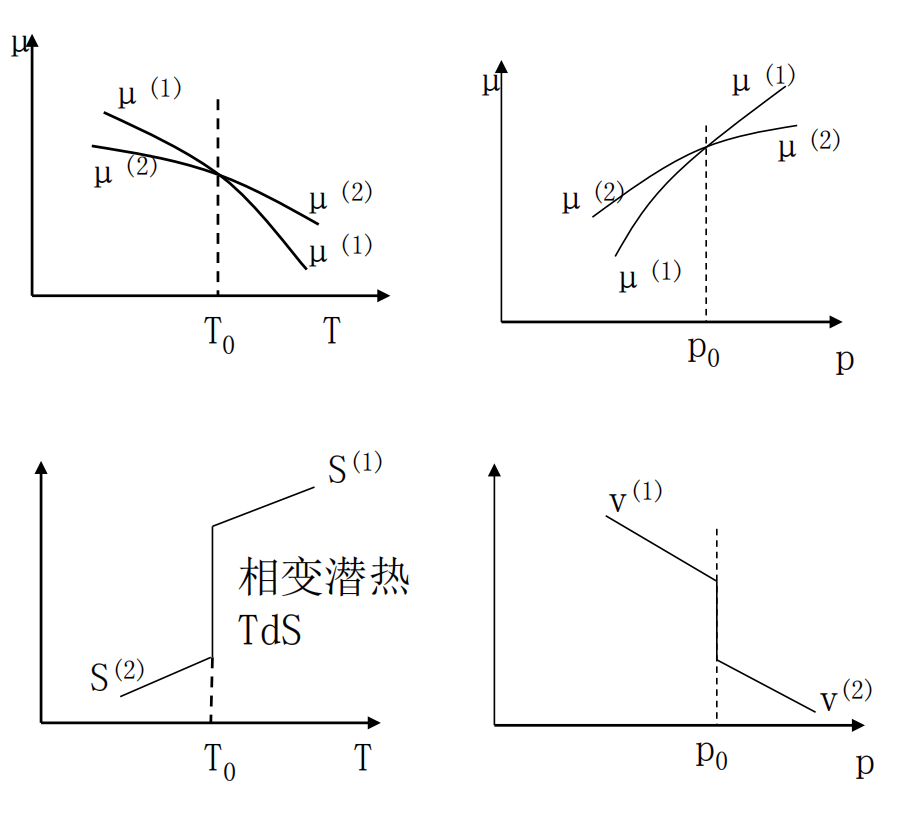
B:二级相变:

s,vs,v连续:

∂μ(1)∂T=∂μ(2)∂T,(s(1)=s(2))∂μ(1)∂p=∂μ(2)∂p,(v(1)=v(2))\frac{\partial \mu^{(1)}}{\partial T}=\frac{\partial \mu^{(2)}}{\partial T}, \quad\left(s^{(1)}=s^{(2)}\right) \quad \frac{\partial \mu^{(1)}}{\partial p}=\frac{\partial \mu^{(2)}}{\partial p}, \quad\left(v^{(1)}=v^{(2)}\right)

但：

∂2μ(1)∂T2≠∂2μ(2)∂T2,∂2μ(1)∂T∂p≠∂2μ(2)∂T∂p,∂2μ(1)∂p2≠∂2μ(2)∂p2,\frac{\partial^2 \mu^{(1)}}{\partial T^2} \neq \frac{\partial^2 \mu^{(2)}}{\partial T^2}, \quad \frac{\partial^2 \mu^{(1)}}{\partial T \partial p} \neq \frac{\partial^2 \mu^{(2)}}{\partial T \partial p}, \quad \frac{\partial^2 \mu^{(1)}}{\partial p^2} \neq \frac{\partial^2 \mu^{(2)}}{\partial p^2},

所以

cp=T(∂s∂T)p=−T∂2μ∂T2α=1v(∂v∂T)p=1v∂2μ∂T∂pκT=−1v(∂v∂p)Tc_p =T\left(\frac{\partial s}{\partial T}\right)_p=-T \frac{\partial^2 \mu}{\partial T^2} \\ \alpha =\frac{1}{v}\left(\frac{\partial v}{\partial T}\right)_p=\frac{1}{v} \frac{\partial^2 \mu}{\partial T \partial p} \\ \kappa_T =-\frac{1}{v}\left(\frac{\partial v}{\partial p}\right)_T

均不连续

二级及以上的相变称为连续相变

艾伦费斯特方程：
二级相变点压强随温度变化的斜率公式(由s,vs,v的连续性易证)

dpdT=α(2)−α(1)κT(2)−κT(1)\frac{d p}{d T}=\frac{\alpha^{(2)}-\alpha^{(1)}}{\kappa_T^{(2)}-\kappa_T^{(1)}}

dpdT=cp(2)−cp(1)Tv(α(2)−α(1))\frac{d p}{d T}=\frac{c_p^{(2)}-c_p^{(1)}}{T v\left(\alpha^{(2)}-\alpha^{(1)}\right)}

3.9 朗道连续相变理论

1937 年朗道(Landau)试图对连续相变提供一
个统一的描述。
他提出了序参量(order parameter)的概念，认为连续相变的特征是：

  • 物质有序程度的改变
  • 与之相伴随的物质对称性质的变化

三维各向同性铁磁体：

  • 铁磁物质的原子具有固有的磁矩，两个相邻原子在其磁矩平行时相互作用能量较低，绝对零度下物质处在能量最低的状态
  • 所有原子的磁矩取向都相同，是磁完全有序的状态
  • 温度升高时，热运功有减弱有序取向的趋势，不过只要温度不太高，仍有为数较多的原子磁矩沿某一取向
  • 铁磁物质存在自发磁化强度M,且M 随温度升高而减小
  • 当温度升高达到临界温度TcT_c时，自发磁化强度减小到零，物质转变为顺磁体

用$M (T) $作为序参量来描述铁磁物质的有序程度

  • 在临界温度以上自发磁化强度为零时，系统是各向同性的，或者说系统具有空间转动的对称性
  • 在临界温度以下自发磁化强度非零时，自发磁化强度向量M 处在空间某个方向而破坏了系统对于空间转动的对称性。

具体讨论单轴各向异性铁磁体：

  • 单轴铁磁体具有一个容易磁化的晶轴，原子磁矩的取向只能平行或反平行于这个晶轴，因此它的序参量M(T)M( T)也只能沿这个轴。
  • M取正值对应于磁矩向上，M取负值对应于磁矩向下，由偶然的因素决定
  • 对于自发磁化强度为零的顺磁状态，上和下两个方向是对称或等价的。对于自发磁化强度非零的铁磁状态，自发磁化强度只能在上、下之中取一个方向。

通常在临界温度以下的相，对称性较低、有序度较高、序参量非零；临界温度以上的相，对称性较高、有序度较低、序参量为零。随着温度的降低，序参量在临界点连续地从零变到非零。

当系统由顺磁状态转变为铁磁状态时，系统的对称性就突然降低了，发生了对称破缺。

以单轴铁磁体为例，介绍朗道的连续相变理论。朗道认为，在临界点Tc附近，序参量M是一个小量，可以将自由能F(T,M)F(T,M)在TCT_C附近按M的幂展开，称为朗道自由能：

F(T,M)=F0(T)+12a(T)M2+14b(T)M4+⋯F(T, M)=F_0(T)+\frac{1}{2} a(T) M^2+\frac{1}{4} b(T) M^4+\cdots

其中F0(T)中F_0(T)是M=0M=0时的自由能。

由于系统对于变换 M⇌−MM \rightleftharpoons-M 是对称的，展开式不含M的奇次幂。

只讨论无外磁场，即H=0的情况，并且假设体积的变化可以忽略。这样状态参量就只有温度T。式中展开系数a(T)和b(T)是温度T的函数。我们将利用在T、V不变的条件下稳定平衡态自由能最小的条件，确定体系的M为温度T的函数。

稳定平衡态下F具有极小值，应有

∂F∂M=M(a+bM2)=0,∂2F∂M2=a+3bM2>0\frac{\partial F}{\partial M}=M\left(a+b M^2\right)=0, \quad \frac{\partial^2 F}{\partial M^2}=a+3 b M^2>0

上式有三个解：

M=0,M=±−abM=0, \quad M= \pm \sqrt{-\frac{a}{b}}

解 M=0M=0 代表无序态，相应于T>TCT>T_C的温度范围，将M=0M=0代入上式可知，在T>TCT>T_C 时 a>0a>0 。上面非零解代表有序态，相应于 T<TCT<T_C 的温度范围。将 MM 的非零解代入上式可知，在 T<TCT<T_C 时 a<0a<0 。序参量在 TCT_C 处连续地由零转变到非零，所以在 T=TCT=T_C 处应有 a=0a=0 。

在临界点的邻域：

a=a0(T−TcTc),a0>0a=a_0\left(\frac{T-T_c}{T_c}\right), \quad a_0>0

因为M=±−abM= \pm \sqrt{-\frac{a}{b}} 应是实数，而在T<TCT<T_C时a<0a<0，故常数b>0b>0

将a和b代入 M=±−abM= \pm \sqrt{-\frac{a}{b}} 可知，在临界点的邻域，单轴铁磁体的自发磁化强度M为

T>Tc,M=0T<Tc,M=±(a0b)1/2(Tc−TTc)1/2\begin{aligned} & T>T_c, M=0 \\ & T<T_c, M= \pm\left(\frac{a_0}{b}\right)^{1 / 2}\left(\frac{T_c-T}{T_c}\right)^{1 / 2} \end{aligned}

由此可知，在 TcT_c的两侧热力学函数各存在一个分支。在 T>TcT>T_c 的无序相 (a>0,b>0)(a>0,b>0), 朗道自由能的极小在 M=0\mathrm{M}=0 处, 即无序相的自由能为 F=F0,T>TcF=F_0, T>T_c

在 T<TcT<T_c 的有序相 (a<0,b>0)(a<0, b>0), 朗道自由能的极小在 M=±−abM= \pm \sqrt{-\frac{a}{b}} 处，即有序相的自由能为 F=F0−a24b,T<TcF=F_0-\frac{a^2}{4 b}, \quad T<T_c

在临界点T=Tc(a=0,b>0)T=T_c (a=0, b>0)，自由能的两个分支重合。

现在讨论铁磁体的零场比热容。利用公式 c=−T∂2F∂T2c=-T \frac{\partial^2 F}{\partial T^2}可得, 在 T=TcT = T_c 处两相比热容之差为

c(T→−Tc)−c(T→+Tc)=a022bTcc\left(T \xrightarrow{-} T_c\right)-c\left(T \xrightarrow{+} T_c\right)=\frac{a_0^2}{2 b T_c}

该式表明，有序相的比热容大于无序相的比热容，且在 T=TcT=T_c 处比热容的突变是有限的。

小结：

  • 作为热力学理论，朗道理论将序参量看作是在整个系统中均匀而没有涨落的。实际上在连续相变临界点的邻域，序参量往往有强烈的涨落。
  • 尽管存在不足，朗道理论仍然是非常重要和成功的理论。在定性分析物质的相结构时有很大价值。由于数学处理简单，面对新的问题，人们往往用朗道理论进行初步地分析。
  • 值得强调，在相对涨落较小的情形，例如低温零磁场下金属正常与超导状态的转变以及液晶中的某种转变，朗道理论 (或推广的朗道理论) 得到的结果与实验结果是相符的。
  • 朗道理论提出了一些重要概念如序参量、对称破缺、普适性等。这些概念在临界现象的现代理论中仍然起着重要作用：
    1）弱电统一理论的Higgs机制；
    2）宇宙的真空相变和暴涨理论；

至此第三章结束