热力学部分习题

一、热力学定律

(1)试根据热力学第二定律证明两条绝热线不能相交。

证明：

假设在P-V图中两条绝热先交于C点，设想一等温线与两条绝热线分别交于A点和B点，因为等温线斜率小于绝热线斜率，这样的等温线总是存在。则在循环ABCA中，气体在等温过程AB中从外界吸取热量Q，在循环过程中对外做功W，其数值等于三条线所围的面积。循环过程完成后，系统回到原来的状态，根据热力学第一定律，有W=Q，这样一来，系统在上述循环过程中就从单一热源吸热并将之完全转化为功了，这就违背了热力学第二定律的开尔文说法，这是不可能的。因此两条绝热线不可能相交。

(2)一摩尔范式气体满足状态方程 $p=\frac{R T}{V-b}-\frac{a}{V^2}$ , 如果它的内能由 $u=c T-\frac{a}{V}$ （ V 为摩尔体积， a 为状态方程常数之一， c 为常数）给出，计算摩尔比热 $c_V$ 和 $c_p$ 。

解:

\begin{gathered} c_V=\left(\frac{\partial u}{\partial T}\right)_V=c \\ c_p=\left(\frac{\partial u}{\partial T}\right)_p+p\left(\frac{\partial V}{\partial T}\right)_p=\left(\frac{\partial u}{\partial T}\right)_V+\left[\left(\frac{\partial u}{\partial V}\right)_T+p\right]\left(\frac{\partial V}{\partial T}\right)_p=c+\left(\frac{a}{V^2}+p\right)\left(\frac{\partial V}{\partial T}\right)_p \end{gathered}

由范德瓦耳斯方程

\left(p+\frac{a}{V^2}\right)(V-b)=R T

求得

\left(\frac{\partial V}{\partial T}\right)_p=\frac{R}{p-\frac{a}{V^2}+\frac{2 a b}{V^3}}

因此

c_p=c+\frac{R\left(p+\frac{a}{V^2}\right)}{p-\frac{a}{V^2}+\frac{2 a b}{V^3}}=c+\frac{R}{1-\frac{2 a(V-b)^2}{R T V^3}}

二、热机效率

（1）空窖辐射系统的温度为 T , 体积为 V 。已知空窖辐射的内能 $U=a V T^4$ , 以及 $P=\frac{1}{3} a T^4$ ，其中 a 为常数。试证明平衡辐射的可逆绝热过程满足 $T^3 V=$ 常量

证明：

由 $d S=\frac{d U+p d V}{T}$ 得 $d S=\frac{1}{T} d\left(a T^4 V\right)+\frac{1}{3} a T^3 d V=\frac{4}{3} a d\left(V T^3\right)$

所以, 积分得 $S=\frac{4}{3} a V T^3$ , 没有积分常量。

可逆绝热过程的熵不变, 所以 $T^3 V=$ 常量

（2）以平衡辐射为工作物质的卡诺循环，请画出 P-V 图并计算其效率。

解:

由 $P=\frac{1}{3} a T^4$ , 平衡辐射等温过程也是等压过程, 又由于 $T^3 V=$ 常量

我们可以得到 $p V^{\frac{4}{3}}=C$ (常量)，因此可以得到下面的平衡辐射可逆卡诺循环的 P - V 图

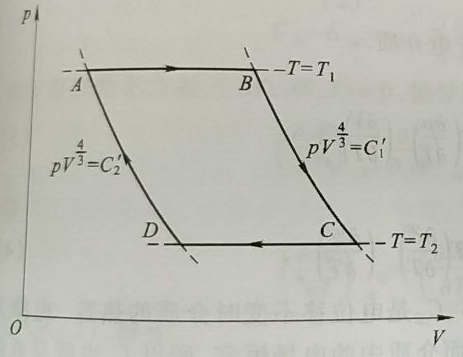
计算热机的效率用下面给出的 T-S 图更方便,

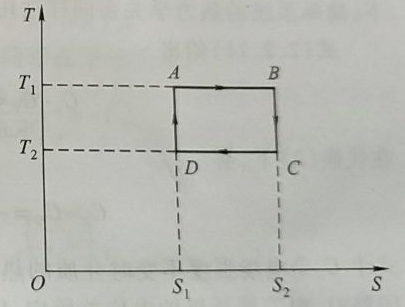
由状态 A 等温膨胀至状态 B , 平衡辐射吸热 $Q_1=T_1\left(S_2-S_1\right)$
由状态 C 等温压缩至状态 D, 平衡辐射放热 $Q_2=T_2\left(S_2-S_1\right)$
循环过程工作物质做功 $W=Q_1-Q_2$
所以效率 $\eta=\frac{W}{Q_1}=1-\frac{T_2}{T_1}$

（3）奥托循环的理想循环由两个绝热过程和两个等容过程组成，求该循环热机的效率 (已知 V1 和 V2)。

解:

$1 \rightarrow 2$ 绝热过程, $\frac{T_2}{T_1}=\left(\frac{V_1}{V_2}\right)^{\gamma-1}; 3 \rightarrow 4$ 绝热过程, $\frac{T_3}{T_4}=\left(\frac{V_1}{V_2}\right)^{\gamma-1}$ .

\frac{T_2}{T_1}=\frac{T_3}{T_4}=\frac{T_3-T_2}{T_4-T_1}

$2 \rightarrow 3$ 等容过程, $Q_1=C_V\left(T_3-T_2\right) ; 4 \rightarrow 1$ 等容过程, $Q_2^{\prime}=C_V\left(T_4-T_1\right)$ .

\eta=\frac{Q_1-Q_2^{\prime}}{Q_1}=1-\frac{Q_2^{\prime}}{Q_1}=1-\frac{T_4-T_1}{T_3-T_2}=1-\frac{T_1}{T_2}=1-\left(\frac{V_2}{V_1}\right)^{\gamma-1}=1-\frac{1}{r^{\gamma-1}}

$r=\frac{V_1}{V_2}$ , 为压缩比

三、热力学性质

已知某单位摩尔气体满足物态方程 $p=\frac{R T}{(V-b)} \exp \left(-\frac{a}{V R T}\right)$ 。
(1) 求该气体的体膨胀系数 $\alpha$ .

解：

由范式气体物态方程得

d p=\exp \left(-\frac{a}{V R T}\right)\left(1+\frac{a}{V R T}\right) \frac{R d T}{(V-b)}-d V\left(\frac{R T}{(V-b)^2}+\frac{a}{(V-b) V^2}\right) \exp \left(-\frac{a}{V R T}\right)

所以

\alpha=\frac{1}{V}\left(\frac{\partial V}{\partial T}\right)_p=\left(1+\frac{a}{V R T}\right)\left(\frac{V T}{(V-b)}+\frac{a}{V R}\right)^{-1}

(2) 求 $\left(\frac{\partial U}{\partial V}\right)_T$

解：

\left(\frac{\partial U}{\partial V}\right)_T=T\left(\frac{\partial p}{\partial T}\right)_V-p=\frac{a}{V(V-b)} \exp \left(-\frac{a}{V R T}\right)

(3) 处于 $0^{\circ} \mathrm{C}$ 的理想气体, 绝热膨胀到原来体积的 10 倍, 计算气体温度的变化。

解:

初态: $P_0 V_0 = RT_0$ , 末态： $P \cdot 10 V_0 = RT$

\begin{gathered} p_0 V_0^\gamma=p\left(10 V_0\right)^\gamma, \quad p_0 V_0 \cdot V_0^{\gamma-1}=p \cdot\left(10 V_0\right) \cdot\left(10 V_0\right)^{\gamma-1} \\ R T_0 \cdot V_0^{\gamma-1}=R T \cdot\left(10 V_0\right)^{\gamma-1}, \quad T_0 \cdot V_0^{\gamma-1}=T \cdot 10^{\gamma-1} \cdot V_0^{\gamma-1} \\ T=10^{1-\gamma} \cdot T_0, \quad \Delta T=T-T_0=10^{1-\gamma} \cdot T_0-T_0=T_0\left(10^{1-\gamma}-1\right) \\ \Delta T=T_0\left(10^{1-\gamma}-1\right)=\left(10^{1-\gamma}-1\right) \times 273.15(\mathrm{~K}) \end{gathered}

四、熵变

有 A 和 B 两个容器, 每个容器内装有 n 摩尔相同的理想气体。初始两个容器彼此孤立,气体温度都为 T , 压强分别为 $\mathrm{P}_A$ 和 $\mathrm{P}_B$ 。现将隔开气体的隔板抽走, 求建立起平衡之后系统的熵变，并证明此熵变不是负值。

解:

初始容器中气体体积分别为 $V_A=\frac{n R T}{P_A}$ 和 $V_B=\frac{n R T}{P_B}$ , 最终体积变为 $V_A+V_B$ ,
最终压强 $p_F=\frac{2 n R T}{V_A+V_B}=\frac{2 p_A p_B}{\left(p_A+p_B\right)}$

等温膨胀过程 $\Delta U=\Delta W+\Delta Q=0$ ,

所以 $\Delta Q=-\Delta W$

而 $\Delta W=\Delta W_A+\Delta W_B=\left(-\int_{\frac{n R T}{P_A}}^{\frac{n R T}{p_F}} \frac{n R T}{V} d V\right)+\left(-\int_{\frac{n R T}{P_B}}^{\frac{n R T}{p_R}} \frac{n R T}{V} d V\right)=-n R T \ln \left(\frac{\left(p_A+p_B\right)^2}{4 p_A p_B}\right)$

所以 $\Delta S=\Delta Q / T=-\Delta W / T=n R \ln \left(\frac{\left(p_A+p_B\right)^2}{4 p_A p_B}\right) \geq 0$

因为 $\left(p_A+p_B\right)^2 \geq 4 p_A p_B$

五、

（1）利用麦氏关系等办法, 证明

A. \left(\frac{\partial T}{\partial p}\right)_H=T\left(\frac{\partial V}{\partial H}\right)_p-V\left(\frac{\partial T}{\partial H}\right)_p

B. \left(\frac{\partial T}{\partial S}\right)_H=\frac{T}{C_p}-\frac{T^2}{V}\left(\frac{\partial V}{\partial H}\right)_p

C.\chi_T / \chi_S=C_\mathscr{H} / C_\mathscr{M}

其中 $\chi_T=\left(\frac{\partial \mathscr{M}}{\partial \mathscr{\mathscr {H }}}\right)_T$ 与 $\chi_S=\left(\frac{\partial \mathscr{M}}{\partial \mathscr{H}}\right)_S$ 分别代表等温与绝热磁化率